DEMOSTRACIÓN FORMAL:
Una demostración formal consiste en mostrar que la conclusión puede derivarse desde las premisas mediante la aplicación de las reglas de inferencia. Para probar que el argumento mostrado más arriba es válido usted necesita dos únicas reglas de inferencia. 1. Silogismo hipotético [HS] 2. Modus Tollens [MT] Un desglose detallado de la demostración formal, para el problema mostrado más arriba, es el siguiente: Paso 1: Desde la línea 1 y la linea 2 nosotros podemos derivar T > L por (HS). HS P > Q (1) T > H Q > R (2) H > L - - ------ ---------- P > Q T > L Usted indica este nuevo paso en la demostración formal añadiendo una cuarta línea justificada con los números de las lineas a las que afectó la aplicación de la regla del HS: 1. T > H 2. H > L 3. ~L /~T 4. T > L 1, 2 (HS) Paso 2: Despues podemos usar la regla del Modus Tollens (MT) para derivar ~T desde líneas 3 y 4. T > L ~L ------ ~T Usted indica este nuevo paso en la demostración formal, añadiendo una quinta linea justificada con los números de las lineas a las que afectó la aplicación de la regla del MT: 1. T > H 2. H > L 3. ~L /~T 4. T > L 1, 2 (HS) 5. ~T 3, 4 (MT) La demostración formal es completa una vez usted ha derivado una línea que es la conclusión.
domingo, 29 de marzo de 2009
lOgiiqa cuantificacional.
Hay argumentos que pueden ser formalizados y resueltos mediante los mecanismos que nos proporciona la lógica de enunciados. sin embargo, existen otros muchos enunciados, que aún siendo elementales no pueden ser resueltos por la lógica de enunciados. Por ejemplo:
- Todo griego es europeo
- Todo ateniense es griego
________________________
- Todo ateniense es europeo
Este argumento es formalmente válido, sin embargo, las estructuras lógicas que lo justifican no son las que se utilizan en la lógica de enunciados, y esto lo podemos observar porque si asignamos una letra proposicional a cada uno de los enunciados, la formulación resultante no resultaría convincente:
-p, q ^ r
Por que no hay ninguna ley de la lógica proposicional que permita concluir ' r' partiendo de las premisas 'p' y 'q'. Esto sucede porque la forma lógica de este argumento no puede ser captada con los medios de la lógica de enunciados. Para captar la forma lógica de estos argumentos es necesario penetrar en la estructura interna de los predicados. Así, en el caso anterior, la pieza clave de la estructura que justifica su validez la forman las palabras "todo" y "algún". Estos términos rebasan el ámbito de la lógica de enunciados.
La Lógica Cuantificacional o Lógica de Predicados, a diferencia de la lógica proposicional, se interna en las proposiciones y las examina por dentro. Esto no quiere decir que la lógica cuantificacional abandone la lógica proposicional. La lógica no puede considerarse como un conjunto de cálculos desperdigados o un conjunto de cálculos superpuestos unos encima de otros de forma que unos sean la negación de los demás. La lógica es más bien una acumulación organizada de cálculos donde cada uno de los cuales supone la integración de los anteriores en un sistema más amplio.
El análisis de la lógica cuantificacional descubre en los enunciados dos cosas fundamentales:
 | Expresiones que se refieren a individuo |
| Expresiones que refieren a propiedades |
| Expresiones que atribuyen propiedades a individuos.[Cuantificadores] |
descripciiOn de elementOs de un argumentO
La argumentación.
-
Argumentar significa defender una idea o una opinión aportando un conjunto de razones que justifiquen nuestra postura.
-
La capacidad para argumentar correctamente suele ir emparejada con la capacidad de influir sobre las personas y es un reflejo de la organización del pensamiento.
-
En toda argumentación podemos distinguir 3 elementos:
-
El objeto, es el tema sobre el cual se argumenta.
-
La tesis, el la postura q el argumentador tiene respecto al tema.
-
Los argumentos, son las razones en las que basamos nuestra postura ante el tema.
valiidez lOgiiqa
Se dice que algo tiene validez lógica porque tiene, y se le reconoce, la cualidad de poseer un valor determinado, o bien la capacidad o eficacia para realizar el valor que se supone ha de tener.
La validez de un cuchillo reside en su cualidad para realizar el valor, la utilidad de "cortar". Cuanto más y mejor corte, mejor realiza el valor que se le supone, su validez.
Respecto a la ciencia y a la filosofía, el valor de referencia es la verdad que, respecto a la validez, adquiere dos sentidos, epistemológico uno y lógico el otro.
tabla de verdad
es una herramienta desarrollada por Charles Peirce en los años 1880, siendo sin embargo más popular el formato que Ludwig Wittgenstein desarrolló en su Tractatus logico-philosophicus, publicado en 1921.
Se emplean en lógica para determinar los posibles valores de verdad de una expresión o proposición molecular. O si un esquema de inferencia, como argumento, es formalmente válido mostrando que, efectivamente, es una tautología.
Considerando dos proposiciones A y B, cada una como un todo (sea como proposición atómica o molecular) y asimismo cada una con sus dos posibles valores de verdad V (Verdadero) y F (Falso), y considerando su relación "$" como variable de cualquier relación sintáctica posible que defina una función de verdad, podrían suceder los casos siguientes:
NOTA: Las proposiciones A, B, C,.... mayúsculas simbolizan cualquier proposición, atómica o molecular, por lo que propiamente son expresiones metalingüísticas respecto al lenguaje objeto de la lógica proposicional, generalmente simbolizadas con minúsculas p, q, r, s... como proposiciones atómicas.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | ||
| A | B | A$B | A$B | A$B | A$B | A$B | A$B | A$B | A$B | A$B | A$B | A$B | A$B | A$B | A$B | A$B | A$B |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| V | V | V | V | V | V | V | V | V | V | F | F | F | F | F | F | F | F |
| V | F | V | V | V | V | F | F | F | F | V | V | V | V | F | F | F | F |
| F | V | V | V | F | F | V | V | F | F | V | V | F | F | V | V | F | F |
| F | F | V | F | V | F | V | F | V | F | V | F | V | F | V | F | V | F |
Las dos primeras columnas de la tabla nos muestran los cuatro casos de combinación posibles según el valor de verdad de A y de B. Tenemos por tanto 4 líneas, y 16 columnas que representan todos los posibles valores que pueden darse según se defina una función de verdad cualquiera.
De esta forma podemos conocer mecánicamente, es decir mediante algoritmo, el valor de verdad de cualquier conexión lógica, siempre y cuando previamente la hayamos definido como función de verdad.
Se hace necesario definir todas las relaciones establecidas por las conexiones en valores de verdad.
- Negación (¬),(~)
Consiste en cambiar el valor de verdad de una variable proposicional.
| A |  |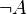
|---|---|
| V | F |
| F | V |
- Conjunción
La proposición molecular será verdadera sólo cuando ambas variables proposicionales sean verdaderas.(Columna 8 de la tabla de funciones posibles)
| A | B |  |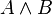
|---|---|---|
| V | V | V |
| V | F | F |
| F | V | F |
| F | F | F |
- Disyunción
La proposición molecular será verdadera cuando una o ambas variables proposicionales sean verdaderas.(Columna 2 de la tabla de funciones posibles)
| A | B |  |
|---|---|---|
| V | V | V |
| V | F | V |
| F | V | V |
| F | F | F |
- Condicional (→)
La proposición molecular será verdadera cuando se cumpla si es verdadero A entonces lo es B. (Columna 5 de la tabla de funciones posibles)
| A | B |  |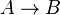
|---|---|---|
| V | V | V |
| V | F | F |
| F | V | V |
| F | F | V |
- Bicondicional (↔, si y sólo si)
La proposición molecular será verdadera cuando ambas variables proposicionales tengan a la vez el mismo valor de verdad. (Columna 7 de la tabla de funciones posibles)
| A | B |  |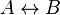
|---|---|---|
| V | V | V |
| V | F | F |
| F | V | F |
| F | F | V |
- Disyunción exclusiva
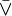
La proposición molecular será verdadera sólo cuando una de las dos variables proposicionales sea verdadera, pero no las dos. (Columna 10 de la tabla de posibles valores)
| A | B |  |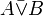
|---|---|---|
| V | V | F |
| V | F | V |
| F | V | V |
| F | F | F |
Tablas de verdad [editar]
Las tablas nos manifiestan los posibles valores de verdad de cualquier proposición molecular, así como el análisis de la misma en función de las proposicíones que la integran, encontrándonos con los siguientes casos:
Verdad Indeterminada o Contingencia [editar]
Se entiende por verdad contingente, o verdad de hecho, aquella proposición que puede ser verdadera o falsa, según los valores de las proposiciones que la integran. Sea el caso: A /\ (B \/ C).
Su tabla de verdad se construye de la siguiente manera:
Ocho filas que responden a los casos posibles que pueden darse según el valor V o F de cada una de las proposiciones A, B, C. (Columnas 1, 2, 3)
Una columna (Columna 4) en la que se establecen los valores de B \/ C aplicando la definición del disyuntor a los valores de B y de C en cada una de las filas.(Columnas 2,3 → 4)
Una columna (columna 5) en la que se establecen los valores resultantes de aplicar la definición de la conjunción entre los valores de A (columna 1) y valores de la columna B \/ C, (columna 4) que representarán los valores de la proposición completa A /\ (B \/ C), cuyo valor de verdad es V o F según la fila de los valores de A, B, y C que consideremos. (Columnas 1,4 → 5)
| 1 | 2 | 3 | 4 | 5 |
| A | B | C | B\/C | A/\(B\/C) |
|---|---|---|---|---|
| V | V | V | V | V |
| V | V | F | V | V |
| V | F | V | V | V |
| V | F | F | F | F |
| F | V | V | V | F |
| F | V | F | V | F |
| F | F | V | V | F |
| F | F | F | F | F |
Donde podemos comprobar cuándo y por qué la proposición A/\(B\/C) es V y cuándo es F
Contradicción [editar]
Se entiende por proposición contradictoria, o contradicción, aquella proposición que en todos los casos posibles de su tabla de verdad su valor siempre es F. Dicho de otra forma, su valor F no depende de los valores de verdad de las proposiciones que la forman, sino de la forma en que están establecidas las relaciones de unas con otras. Sea el caso: [(A/\B)/\¬(A\/B)]/\C
Procederemos de manera similar al caso anterior. Aplicamos (Columna 4) la definición de conjuntor a los valores de A y B.(columnas 1,2 → 4) Después aplicamos la definición de disyuntor a los valores de A y B. (columnas 1,2 → 5) Aplicamos en la columna siguiente (Columna 6) el negador a los valores de la columna anterior. Aplicamos el conjuntor a los valores de la columna (A/\B)(Columna 4) con los de la columna ¬(A\/B).(Columna 6) Por último (Columna 8) aplicamos el conjuntor a los valores de la columna de C (Columna 3) con la columna última (Columna 7)cuyo resultado nos da los valores de [(A/\B)/\¬(A\/B)]/\C, siempre falsos cualquiera que sea la fila que consideremos.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| A | B | C | A/\B | A\/B | ¬(A\/B) | (A/\B)/\¬(A\/B) | [(A/\B)/\¬(A\/B)]/\C |
|---|---|---|---|---|---|---|---|
| V | V | V | V | V | F | F | F |
| V | V | F | V | V | F | F | F |
| V | F | V | F | V | F | F | F |
| V | F | F | F | V | F | F | F |
| F | V | V | F | V | F | F | F |
| F | V | F | F | V | F | F | F |
| F | F | V | F | F | V | F | F |
| F | F | F | F | F | V | F | F |
Tautologías [editar]
Se entiende por proposición tautológica, o tautología, aquella proposición que en todos los casos posibles de su tabla de verdad su valor siempre es V. Dicho de otra forma, su valor V no depende de los valores de verdad de las proposiciones que la forman, sino de la forma en que están establecidas las relaciones sintácticas de unas con otras. Sea el caso: [(A→B)/\(B→C)] →(A→C)
Siguiendo la mecánica algorítmica de la tabla anterior construiremos su tabla de verdad:
| A | B | C | A→B | B→C | (A→B)/\(B→C) | (A→C) | [(A→B)/\(B→C)] →(A→C) |
|---|---|---|---|---|---|---|---|
| V | V | V | V | V | V | V | V |
| V | V | F | V | F | F | F | V |
| V | F | V | F | V | F | V | V |
| V | F | F | F | V | F | F | V |
| F | V | V | V | V | V | V | V |
| F | V | F | V | F | F | V | V |
| F | F | V | V | V | V | V | V |
| F | F | F | V | V | V | V | V |
Tablas de verdad, proposiciones lógicas y argumentos deductivos [editar]
En realidad toda la lógica está contenida en las tablas de verdad, en ellas se nos manifesta todo lo que implican las relaciones sintácticas entre las diversas proposiciones.
No obstante la sencillez del algoritmo, aparecen dos dificultades.
- La gran cantidad de operaciones que hay que hacer para una proposición con más de 4 variables.
Esta dificultad ha sido magníficamente superada por la rapidez de los ordenadores, y no presenta dificultad alguna.
- Que únicamente será aplicable a un esquema de inferencia, o argumento cuando la proposición condicionada, como conclusión, sea previamente conocida, al menos como hipótesis, hasta comprobar que su tabla de verdad manifiesta una tautología.
Por ello se construye un cálculo mediante cadenas deductivas:
Las proposiciones que constituyen el antecedente del esquema de inferencia, se toman como premisas de un argumento.
Se establecen como reglas de cálculo algunas tautologías como tales leyes lógicas, (pues garantizan, por su carácter tautológico, el valor V).
Se permite la aplicación de dichas reglas como reglas de sustitución de fórmulas bien formadas en las relaciones que puedan establecerse entre dichas premisas.
Deduciendo mediante su aplicación, como teoremas, todas las conclusiones posibles que haya contenidas en las premisas.
Cuando en un cálculo se establecen algunas leyes como principios o axiomas, el cálculo se dice que es axiomático.
El cálculo lógico así puede utilizarse como demostración argumentativa.
Aplicaciones [editar]
La aplicación más importante de las tablas de verdad procede del hecho de que, interpretando los valores lógicos de verdad como 1 y 0 en el sentido:
Valor 1: corriente eléctrica
Valor 0: ausencia de dicha corriente.
Los valores de entrada o no entrada de corriente a través de un diodo puede producir una salida 0 o 1 según unas condiciones definidas como función según las tablas definidas anteriormente.
Así se establecen las siguientes funciones: AND, NAND, OR, XOR NOR, que se corresponden con las funciones definidas en las columnas, 8, 9, 2, 10 Y 15 respectivamente, y la función NOT.
En lugar de variables proposicionales consideramos gráficamente los posibles input como EA, EB, y los correspondientes outputs de SALIDA como 1, 0.
NOT
| EA | EB |
|---|---|
| 1 | 0 |
| 0 | 1 |
| EA | EB | AND | NAND | OR | XOR | NOR |
|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 1 | 1 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 |
Esta aplicación hace posible la construcción de aparatos capaces de realizar estas computaciones a velocidades increíbles, llamadas por lo mismo computadoras u ordenadores.
El desarrollo de estos circuitos y su estructuración merece verse en el artículo puerta lógica.
La Tabla de la verdad es una herramienta imprescindible en la recuperación de datos en las bases de datos como Internet con los motores de búsqueda o en una biblioteca con sus ficheros informatizados. Asimismo se utilizan para programar simulaciones lógicas de inteligencia artificial con lenguajes propios. También en modelos matemáticos predictores: meteorología, marketing y otros muchos.
reglas siintactiicas
La Sintáctica corresponde al análisis de la relación existente entre los distintos símbolos o signos del lenguaje.
Reglas Sintácticas
Son los métodos de produccion de sentencias o instrucciones válidas que permitir y dan formar a un programa. las reglas sintácticas permiten reconocer si una cadena o serie de símbolos es correcta gramaticalmente y a su vez información sobre su significado o semántica.
lenguaje siimbOliiqo de la lOgiiqa prOfesiional
En la práctica, no es posible razonar directamente mediante conocimientos en un estado mental, sino por medio de representaciones simbólicas, que se expresan en objetos materiales perceptibles por medio de los sentidos, tales como palabras, signos, gráficos, fórmulas, etc.
El uso del lenguaje corriente lleva implícito un enfoque de sintaxis, que consiste en las relaciones formales entre los términos empleados; y un enfoque semántico, que consiste en el sentido de referencia que se atribuye a las palabras empleadas, su relación con los objetos y los conceptos de la realidad a que con su empleo se trata de aludir, y que es cierto modo es socialmente cambiante dentro de un mismo idioma, considerando distintos tiempos y lugares.
El lenguaje de uso corriente - tanto el coloquial como el culto, literario o el de ciertas disciplinas especializadas - resulta totalmente imperfecto en cuanto al rigor, claridad, abstracción y precisión requerido para la expresión de los conceptos y objetos en los estudios lógicos; especialmente considerando lo expuesto en cuanto a la prescindencia de los componentes de contenidos materiales de los procesos del razonamiento.
En función de ello, la lógica formal procura liberarse de la incidencia que, en cuanto al examen de las cuestiones formales del razonamiento, pueda tener el uso de términos de los lenguajes idiomáticos, creando para ser aplicado en el estudio y exposición de las leyes lógicas, un lenguaje simbólico propio, un lenguaje formal.
Este lenguaje simbólico propio de la lógica, tiene por otra parte la ventaja de su universalidad; en cuanto al prescindir del empleo de expresiones de un idioma real, permite su comprensión directa independientemente del idioma concreto de la persona que se aplique a su estudio.
Ese lenguaje simbólico es además lo que se denomina un metalenguaje, en el sentido de que se lo concibe como una forma de expresión que está “más allá” del uso mismo del lenguaje. En este sentido, se dice que el lenguaje-objeto es el que se utiliza, en tanto que el metalenguaje es aquel con el que se habla del otro; como cuando se aprende un idioma extranjero utilizando para ello el idioma propio.
Una expresión sencilla del lenguaje simbólico aplicable al análisis lógico puede ser similar al aplicado en matemáticas para representar una variable. De esta forma,
|
De esta manera, la sustitución de una proposición por un síimbolo permite construir una teoría de las formas del razonamiento en las cuales intervengan componentes similares; de modo que sea posible reconocer facilmente en un proceso de razonamiento la presencia de una misma proposición, de un mismo concepto, o de una misma propiedad o atributo.
Suscribirse a:
Entradas (Atom)