Se emplean en lógica para determinar los posibles valores de verdad de una expresión o proposición molecular. O si un esquema de inferencia, como argumento, es formalmente válido mostrando que, efectivamente, es una tautología.
Considerando dos proposiciones A y B, cada una como un todo (sea como proposición atómica o molecular) y asimismo cada una con sus dos posibles valores de verdad V (Verdadero) y F (Falso), y considerando su relación "$" como variable de cualquier relación sintáctica posible que defina una función de verdad, podrían suceder los casos siguientes:
NOTA: Las proposiciones A, B, C,.... mayúsculas simbolizan cualquier proposición, atómica o molecular, por lo que propiamente son expresiones metalingüísticas respecto al lenguaje objeto de la lógica proposicional, generalmente simbolizadas con minúsculas p, q, r, s... como proposiciones atómicas.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | ||
| A | B | A$B | A$B | A$B | A$B | A$B | A$B | A$B | A$B | A$B | A$B | A$B | A$B | A$B | A$B | A$B | A$B |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| V | V | V | V | V | V | V | V | V | V | F | F | F | F | F | F | F | F |
| V | F | V | V | V | V | F | F | F | F | V | V | V | V | F | F | F | F |
| F | V | V | V | F | F | V | V | F | F | V | V | F | F | V | V | F | F |
| F | F | V | F | V | F | V | F | V | F | V | F | V | F | V | F | V | F |
Las dos primeras columnas de la tabla nos muestran los cuatro casos de combinación posibles según el valor de verdad de A y de B. Tenemos por tanto 4 líneas, y 16 columnas que representan todos los posibles valores que pueden darse según se defina una función de verdad cualquiera.
De esta forma podemos conocer mecánicamente, es decir mediante algoritmo, el valor de verdad de cualquier conexión lógica, siempre y cuando previamente la hayamos definido como función de verdad.
Se hace necesario definir todas las relaciones establecidas por las conexiones en valores de verdad.
- Negación (¬),(~)
Consiste en cambiar el valor de verdad de una variable proposicional.
| A | 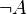 |
|---|---|
| V | F |
| F | V |
- Conjunción

La proposición molecular será verdadera sólo cuando ambas variables proposicionales sean verdaderas.(Columna 8 de la tabla de funciones posibles)
| A | B | 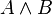 |
|---|---|---|
| V | V | V |
| V | F | F |
| F | V | F |
| F | F | F |
- Disyunción

La proposición molecular será verdadera cuando una o ambas variables proposicionales sean verdaderas.(Columna 2 de la tabla de funciones posibles)
| A | B |  |
|---|---|---|
| V | V | V |
| V | F | V |
| F | V | V |
| F | F | F |
- Condicional (→)
La proposición molecular será verdadera cuando se cumpla si es verdadero A entonces lo es B. (Columna 5 de la tabla de funciones posibles)
| A | B | 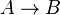 |
|---|---|---|
| V | V | V |
| V | F | F |
| F | V | V |
| F | F | V |
- Bicondicional (↔, si y sólo si)
La proposición molecular será verdadera cuando ambas variables proposicionales tengan a la vez el mismo valor de verdad. (Columna 7 de la tabla de funciones posibles)
| A | B | 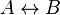 |
|---|---|---|
| V | V | V |
| V | F | F |
| F | V | F |
| F | F | V |
- Disyunción exclusiva
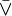
La proposición molecular será verdadera sólo cuando una de las dos variables proposicionales sea verdadera, pero no las dos. (Columna 10 de la tabla de posibles valores)
| A | B | 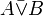 |
|---|---|---|
| V | V | F |
| V | F | V |
| F | V | V |
| F | F | F |
Tablas de verdad [editar]
Las tablas nos manifiestan los posibles valores de verdad de cualquier proposición molecular, así como el análisis de la misma en función de las proposicíones que la integran, encontrándonos con los siguientes casos:
Verdad Indeterminada o Contingencia [editar]
Se entiende por verdad contingente, o verdad de hecho, aquella proposición que puede ser verdadera o falsa, según los valores de las proposiciones que la integran. Sea el caso: A /\ (B \/ C).
Su tabla de verdad se construye de la siguiente manera:
Ocho filas que responden a los casos posibles que pueden darse según el valor V o F de cada una de las proposiciones A, B, C. (Columnas 1, 2, 3)
Una columna (Columna 4) en la que se establecen los valores de B \/ C aplicando la definición del disyuntor a los valores de B y de C en cada una de las filas.(Columnas 2,3 → 4)
Una columna (columna 5) en la que se establecen los valores resultantes de aplicar la definición de la conjunción entre los valores de A (columna 1) y valores de la columna B \/ C, (columna 4) que representarán los valores de la proposición completa A /\ (B \/ C), cuyo valor de verdad es V o F según la fila de los valores de A, B, y C que consideremos. (Columnas 1,4 → 5)
| 1 | 2 | 3 | 4 | 5 |
| A | B | C | B\/C | A/\(B\/C) |
|---|---|---|---|---|
| V | V | V | V | V |
| V | V | F | V | V |
| V | F | V | V | V |
| V | F | F | F | F |
| F | V | V | V | F |
| F | V | F | V | F |
| F | F | V | V | F |
| F | F | F | F | F |
Donde podemos comprobar cuándo y por qué la proposición A/\(B\/C) es V y cuándo es F
Contradicción [editar]
Se entiende por proposición contradictoria, o contradicción, aquella proposición que en todos los casos posibles de su tabla de verdad su valor siempre es F. Dicho de otra forma, su valor F no depende de los valores de verdad de las proposiciones que la forman, sino de la forma en que están establecidas las relaciones de unas con otras. Sea el caso: [(A/\B)/\¬(A\/B)]/\C
Procederemos de manera similar al caso anterior. Aplicamos (Columna 4) la definición de conjuntor a los valores de A y B.(columnas 1,2 → 4) Después aplicamos la definición de disyuntor a los valores de A y B. (columnas 1,2 → 5) Aplicamos en la columna siguiente (Columna 6) el negador a los valores de la columna anterior. Aplicamos el conjuntor a los valores de la columna (A/\B)(Columna 4) con los de la columna ¬(A\/B).(Columna 6) Por último (Columna 8) aplicamos el conjuntor a los valores de la columna de C (Columna 3) con la columna última (Columna 7)cuyo resultado nos da los valores de [(A/\B)/\¬(A\/B)]/\C, siempre falsos cualquiera que sea la fila que consideremos.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| A | B | C | A/\B | A\/B | ¬(A\/B) | (A/\B)/\¬(A\/B) | [(A/\B)/\¬(A\/B)]/\C |
|---|---|---|---|---|---|---|---|
| V | V | V | V | V | F | F | F |
| V | V | F | V | V | F | F | F |
| V | F | V | F | V | F | F | F |
| V | F | F | F | V | F | F | F |
| F | V | V | F | V | F | F | F |
| F | V | F | F | V | F | F | F |
| F | F | V | F | F | V | F | F |
| F | F | F | F | F | V | F | F |
Tautologías [editar]
Se entiende por proposición tautológica, o tautología, aquella proposición que en todos los casos posibles de su tabla de verdad su valor siempre es V. Dicho de otra forma, su valor V no depende de los valores de verdad de las proposiciones que la forman, sino de la forma en que están establecidas las relaciones sintácticas de unas con otras. Sea el caso: [(A→B)/\(B→C)] →(A→C)
Siguiendo la mecánica algorítmica de la tabla anterior construiremos su tabla de verdad:
| A | B | C | A→B | B→C | (A→B)/\(B→C) | (A→C) | [(A→B)/\(B→C)] →(A→C) |
|---|---|---|---|---|---|---|---|
| V | V | V | V | V | V | V | V |
| V | V | F | V | F | F | F | V |
| V | F | V | F | V | F | V | V |
| V | F | F | F | V | F | F | V |
| F | V | V | V | V | V | V | V |
| F | V | F | V | F | F | V | V |
| F | F | V | V | V | V | V | V |
| F | F | F | V | V | V | V | V |
Tablas de verdad, proposiciones lógicas y argumentos deductivos [editar]
En realidad toda la lógica está contenida en las tablas de verdad, en ellas se nos manifesta todo lo que implican las relaciones sintácticas entre las diversas proposiciones.
No obstante la sencillez del algoritmo, aparecen dos dificultades.
- La gran cantidad de operaciones que hay que hacer para una proposición con más de 4 variables.
Esta dificultad ha sido magníficamente superada por la rapidez de los ordenadores, y no presenta dificultad alguna.
- Que únicamente será aplicable a un esquema de inferencia, o argumento cuando la proposición condicionada, como conclusión, sea previamente conocida, al menos como hipótesis, hasta comprobar que su tabla de verdad manifiesta una tautología.
Por ello se construye un cálculo mediante cadenas deductivas:
Las proposiciones que constituyen el antecedente del esquema de inferencia, se toman como premisas de un argumento.
Se establecen como reglas de cálculo algunas tautologías como tales leyes lógicas, (pues garantizan, por su carácter tautológico, el valor V).
Se permite la aplicación de dichas reglas como reglas de sustitución de fórmulas bien formadas en las relaciones que puedan establecerse entre dichas premisas.
Deduciendo mediante su aplicación, como teoremas, todas las conclusiones posibles que haya contenidas en las premisas.
Cuando en un cálculo se establecen algunas leyes como principios o axiomas, el cálculo se dice que es axiomático.
El cálculo lógico así puede utilizarse como demostración argumentativa.
Aplicaciones [editar]
La aplicación más importante de las tablas de verdad procede del hecho de que, interpretando los valores lógicos de verdad como 1 y 0 en el sentido:
Valor 1: corriente eléctrica
Valor 0: ausencia de dicha corriente.
Los valores de entrada o no entrada de corriente a través de un diodo puede producir una salida 0 o 1 según unas condiciones definidas como función según las tablas definidas anteriormente.
Así se establecen las siguientes funciones: AND, NAND, OR, XOR NOR, que se corresponden con las funciones definidas en las columnas, 8, 9, 2, 10 Y 15 respectivamente, y la función NOT.
En lugar de variables proposicionales consideramos gráficamente los posibles input como EA, EB, y los correspondientes outputs de SALIDA como 1, 0.
NOT
| EA | EB |
|---|---|
| 1 | 0 |
| 0 | 1 |
| EA | EB | AND | NAND | OR | XOR | NOR |
|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 1 | 1 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 |
Esta aplicación hace posible la construcción de aparatos capaces de realizar estas computaciones a velocidades increíbles, llamadas por lo mismo computadoras u ordenadores.
El desarrollo de estos circuitos y su estructuración merece verse en el artículo puerta lógica.
La Tabla de la verdad es una herramienta imprescindible en la recuperación de datos en las bases de datos como Internet con los motores de búsqueda o en una biblioteca con sus ficheros informatizados. Asimismo se utilizan para programar simulaciones lógicas de inteligencia artificial con lenguajes propios. También en modelos matemáticos predictores: meteorología, marketing y otros muchos.
Está casi todo bien, sólo trata de arreglar la tabla de al principio, ya que sólo se ve hasta el 10 ;W;
ResponderEliminarTe agradecería mucho eso.
ser inteligente es lo maximo
ResponderEliminarEres muy inteligente mi pequeño saltamontes
EliminarEres muy inteligente pero una buena persona que nos ayuda
EliminarEste comentario ha sido eliminado por el autor.
ResponderEliminarYyyy
Eliminarmuy completo te agrasco la ayuda
ResponderEliminarEs una ofensa en cuanto a propiedad intelectual se refiere... Gran parte del contenido se extrae de Wikipedia y no se cita
ResponderEliminarEsta muy de la verga
ResponderEliminarSabe mucho est@ señor@
ResponderEliminar